当我们在谈论 DRL：从AC、PG 到 A3C、DDPG

本系列意在长期连载分享，内容上可能也会有所增删改减； 因此如果转载，请务必保留源地址，非常感谢！ 知乎专栏：当我们在谈论数据挖掘 引言 在"当我们在谈论 DRL：从Q-learning到DQN"中，我们简单回顾了 RL 的基础知识，并介绍了结合 RL 与 DL 的 DQN。其中介绍的算法基本都是先计算出 Value Function， 然后依靠某种规则得到 Policy。在本篇中，我们聚焦于那些直接对 Policy 进行参数化并优化的方法，即 Policy Based 算法。其中有些算法会需要同时对 Policy 和 Value Function 进行参数化并计算，即 Actor Critic 算法。 需要解释的是，由于我希望对 Policy Based 算法有个较系统的梳理，所以本文涉及的知识点会比较多；但限于篇幅，不会对每个细节进行详细的介绍。这里先给出一张 RL 算法分类/演进示意图（图出自强化学习（Reinforcement Learning）的方法分类）。需要深入理解相关知识的同学可以按图索骥。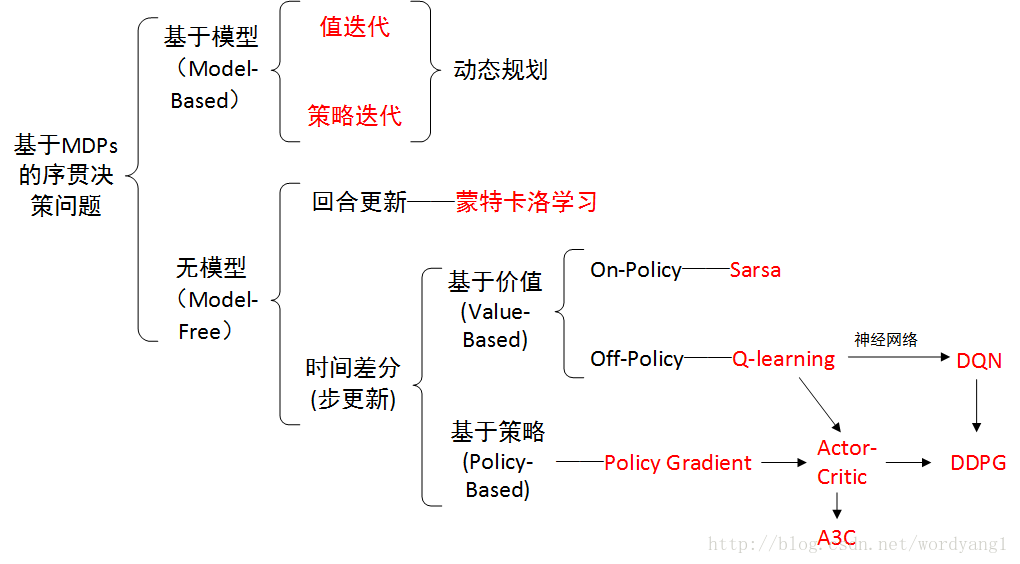 Policy Approximation 这里我们用 \pi(a|s, \theta) 表示参数化的 Policy ，其中 \theta 为需要优化的参数，即 \pi(a|s, \theta) = P[A_t=a|S_t =s, \theta_t=\theta] 于是通过提升/降低某些 P(a|s) 我们就能对 Policy 进行调整，即优化 Policy 成为了优化 \theta 的问题。 对离散 Action，我们一般可以使用 softmax 来计算 \pi(a|s, \theta) ，其中 h(s, a, \theta) 可以看作对此状态的倾向 \pi(a|s, \theta) = \frac{exp(h(s, a, \theta))}{\sum_b exp(h(s, a, \theta))} Policy Gradient 我们将优化目标 \eta 定义为 \eta(\theta) = v_{\pi_{\theta}}(s_0) 其中 v_{\pi_{\theta}} 表示 \pi_{\theta} 的 Value Function，于是有 \frac{\partial \eta}{\partial \theta} = \frac{\partial \eta}{\partial \pi}\frac{\partial \pi}{\partial \theta} 由于 \eta(\pi) 的解析式一般很难求解，计算其梯度自然也是不太可能的。幸运的是，Sutton 在 "Policy gradient methods for reinforcement learning with function approximation. 2000"给出了更加简易的求解式，并将 \nabla \eta(\theta) 与 q(s,a) 联系了起来，即影响深远的 Policy Gradient Theorem，如下 \begin{align} \nabla \eta(\theta) &= \nabla v_{\pi_{\theta}}(s_0) \\ &= \sum_s \sum_{k=0}^{\infty}{\gamma^k P(s_0 \rightarrow s,k,\pi)} \sum_\alpha \nabla \pi(a|s) q_\pi(s,a)\\ &= \sum_s d_\pi(s) \sum_a \nabla \pi(a|s) q_\pi(s,a) \\ \end{align} 其中， P(s_0 \rightarrow s,k,\pi) 表示当起始状态为 s_0 ，通过 Policy \pi 执行 k 轮后，状态为 s 的概率。 d_\pi(s) 表示此折扣型回报条件下的折扣分布。此式的证明可以参考原文或《reinforcement learning :an introduction》的 Section 13.2，此处不再赘述。 有了 \nabla \eta(\theta) ，我们就能根据梯度下降来更新 \theta （使 \eta 增长最快的方向）。 REINFORCE 算法 Policy Gradient Theorem 虽然简化了 \nabla \eta(\theta) 的计算，但一般 d_\pi(s) 仍然是未知的。观察公式可以看出， d_\pi(s) 其实是加权的概率，若我们将折扣因子提出来后，剩余部分则可以通过采样的方式来近似，即 \begin{align} \nabla \eta(\theta) &= \sum_s d_\pi(s) \sum_a q_\pi(s,a) \nabla_\theta \pi(a|s,\theta) \\ &= E_\pi[\gamma^t \sum_a q_\pi(S_t,a) \nabla_\theta \pi(a|S_t,\theta)] \\ \end{align} 可以看出， \nabla \eta(\theta) 已经可以通过采样来计算。但是这样每次计算梯度都需要采样多个 Action，效率比较低，若我们仅采样一个 Action 用于估计其期望，有 \begin{align} \nabla \eta(\theta) &= E_\pi[\gamma^t \sum_a \pi(a|S_t,\theta) q_\pi(S_t,a) \frac{\nabla_\theta \pi(a|S_t,\theta)}{\pi(a|S_t,\theta)}] \\ &= E_\pi[\gamma^t q_\pi(S_t,A_t) \nabla_\theta log \pi(A_t|S_t,\theta)] \\ &= E_\pi[\gamma^t G_t \nabla_\theta log \pi(a|S_t,\theta)] \\ \end{align} 至此，我们每步仅需要采样一个 Action 即可估算梯度。这就是 Williams 在"Simple statistical gradient-following algorithms for connectionist reinforcement learning. 1992"提出的 REINFORCE 算法，其具体步骤如下 可以看出，REINFORCE 算法是典型的 Monte-Carlo 算法，因此也就拥有 MC 算法的特点：很好的收敛性，但收敛较慢；只能处理有终止 State 的任务，且较高的 Variance。 也有简单的办法减少 REINFORCE 算法的 Variance，即 REINFORCE with Baseline。由于 \sum_a b(s) \nabla_\theta \pi(a|s,\theta) = b(s) \nabla_\theta \sum_a \pi(a|s,\theta) = b(s) \nabla_\theta 1 = 0 其中 b(s) 是一个与 a 无关的变量，于是有 \nabla \eta(\theta) = \sum_s d_\pi(s) \sum_a (q_\pi(s,a)-b(s)) \nabla_\theta \pi(a|s,\theta) 通常，可以将 b(s) 设置为 v(S_t, w) 。然后在优化的过程中，同时更新参数 w,\theta ，实现对 v(s),\pi(s) 的求解。REINFORCE with Baseline 具体的流程如下 Actor Critic Actor Critic 是一类算法的统称，从概念上跟以前介绍的 GAN 很像，包含两个模块：Actor（执行器）和 Critic（评价器）。其中，Critic 用于评价当前状态，具体来说就是 bootstrap 地估计 Value Function；而 Actor 用于改进当前 Policy，即根据 Value Function 来更新 Policy 参数。凡是有此类性质的算法都属于 Actor Critic 算法。 上面介绍的 REINFORCE 算法虽然也同时学习了 Policy 和 Value Function，但它并不属于 Actor Critic。原因在于，它学习出的 Value Function 只是作为 baseline，而不是用于 bootstrap。 比如，将上述 REINFORCE with Baseline 算法修改为 Actor Critic 形式，可以将 G_t 用 One Step Return 来替代，则有 Deterministic Policy Gradient 上面我们介绍的都是 Stochastic Policy，即采取的 Action 是不确定的，如上面所写 \pi(a|s, \theta) = P[A_t=a|S_t =s, \theta_t=\theta] 对 Stochastic Policy 计算题度时，如上述公式所述 \nabla \eta(\theta) = \sum_s d_\pi(s) \sum_a q_\pi(s,a) \nabla_\theta \pi(a|s,\theta) 即必须同时对 State 空间和 Action 空间进行采样，对于高维 Action 空间任务，代价是很大的。 Deterministic Policy Gradient 由 Silver 在"Deterministic policy gradient algorithms. 2014"中提出。对于 Deterministic Policy，State 与 Action 的映射关系是确定的，写作 a = \mu_\theta(s) 按常理推断，如果 Deterministic Policy 的梯度也存在的话，其计算应该只需要对 State 空间采样即可。这能显著提高 Action 空间较大的任务的优化，如典型的机器人任务。不过为了达到能对 Environment 进行探索的目的，可以借助 Actor Critic 与 Off Policy。 如前文所说，Off Policy 即 Actor 和 Critic 的 Policy 是不一样的，即 \beta(s) \ne \mu(s) 。于是我们可以将优化目标定义为 Target policy 的 Value Function 的积分，并且根据 Behavior policy 进行加权，有 \begin{align} J_\beta(\mu_\theta) &= \int_S \rho^\beta(s)V^\mu(s)ds \\ &= \int_S \rho^\beta(s)Q^\mu(s, \mu_\theta(s))ds \\ \end{align} 根据论文推导，梯度的计算为 \begin{align} \nabla_\theta J_\beta(\mu_\theta) &\approx \int_S \rho^\beta(s) \nabla_\theta \mu_\theta(a|s) Q^\mu(s,a)ds \\ &= E_{s\sim \rho^\beta}[\nabla_\theta \mu_\theta(s) \nabla_a Q^\mu(s,a) |_{a=\mu_\theta(s)}] \\ \end{align} 可以看出，梯度计算已经不需要对 Action 进行采样了。具体的推导比较复杂，这里就不再展开，建议参考原文。 Deep Deterministic Policy Gradient 与 DQN 一样，有学者尝试将 DPG 与 DL 结合，于是有了"Continuous control with deep reinforcement learning. 2015"中的 DDPG。DDPG 与 DPG 的最主要区别就在于利用神经网络来学习 \mu(s) 与 Q(s,a) 。 在 DQN 中对 Q(s,a) 的学习方法概括下来就是： \begin{align} & \mu(s) = argmax_a Q(s,a) \\ & Q^*(s,a) = r + \gamma Q(s',\mu'(s');\theta^{Q'}) \\ & L(\theta^Q) = E_{s,a,r}[(Q^*(s,a) - Q(s,a;\theta^Q))^2] \\ \end{align} 其中， Q^*(s,a) 为我们期望学习的目标。虽然DQN 本身已经能处理大规模连续空间的问题，但是按照作者的说法，每一步都求解 \mu(s) = argmax_a Q(s,a) 的效率是很低的。如果能直接求解 \mu(s) 那么效率就大大提升了。 于是可结合上文所述的 Policy Gradient 方法，刚好我们在 DPG 中已经有了求解 \mu(s) 的算法，即 \nabla_{\theta^\mu} J \approx E_{s\sim \rho^\beta}[\nabla_{\theta^\mu} \mu(s|\theta^\mu) \nabla_a Q(s,a|\theta^Q) |_{a=\mu(s)}] 接下来，就是将 \mu(s;\theta^\mu) 与 Q(s,a;\theta^Q) 利用神经网络来表示，并利用梯度下降来更新。由于整套方案几乎就是融合了 DQN 和 DPG，具体细节不再赘述，可以参考相关章节。其步骤如下 A3C A3C(Asynchronous Advantage Actor-Critic) 是 DeepMind 在"Mnih V, Badia A P, Mirza M, et al. Asynchronous Methods for Deep Reinforcement Learning. 2016"中提出的一种 DRL 算法，主要优势在于大大提高了训练的效率。同时A3C也代表着一种新的 Actor Critic 算法训练框架，可以与不同的 RL 算法结合使用，具有很强的扩展性。下面我们详细介绍一下 A3C 中的 Value Function 作者首先定义了Advantage A 如下 A(s,t) = Q(s,a)-V(s) 这里 A 可以理解为采用当前 Action 得到的 Q(s,a) 比平均 Value Function V(s) 要优秀多少，这也是为什么叫做 Advantage。 Q(s,t), A(s,t) 的估计可以通过采样获得，即 \begin{align} & Q(s,t) = r + \gamma V(s') \\ & A(s,t) = Q(s,a)-V(s) = r + \gamma V(s') - V(s) \\ \end{align} 其中， V(s) 需要用网络来学习。 当然，上述 Q(s,t) 是 One Step 的，而 A3C 中作者使用的是 N Step，即 Q(s,t) = r_t + \gamma r_{t+1} + ... + \gamma^{n-1} r_{t+n-1} + \gamma^n V(s') 按照作者的说法，N Step 中单次 Reward r 能直接影响先前 n 个 pairs，可以加速收敛。 A3C 中的 Policy A3C 中 \pi(a|s) 也需要用网络来学习。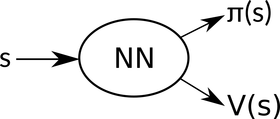在 REINFORCE with Baseline 部分，我们提到过 \nabla \eta(\theta) = \sum_s d_\pi(s) \sum_a (q_\pi(s,a)-b(s)) \nabla_\theta \pi(a|s,\theta) 通常， b(s) 被设置为 Value Function v(s) ，于是公式可以写成 \nabla_\theta \eta = \sum_s d_\pi(s) \sum_a A(s,a) \nabla_\theta \pi(a|s) A3C 中的 Actor Critic 如上述所说， \pi(a|s),V(s) 都用网络来表示，即 其中，则 \pi 作为 Actor，需要学习出更优秀的 Policy；而 V(s) 为 Critic，需要学习出更准确的 Value Function 对现状进行评价。 A3C中的 Asynchronous 训练框架 在"当我们在谈论 DRL：从Q-learning到DQN"的 DQN 部分，我们介绍了利用 Experience Replay 来减少训练数据相关性，来提高训练效果的方法。在 A3C 中，作者利用多线程并行（异步）地对环境进行探索，分别产生训练数据。不同线程的数据天然是不相关的，自然也就不再需要 Experience Replay 了。同时，异步探索使得采样速度更快、分布更加均匀，也能提高训练效果。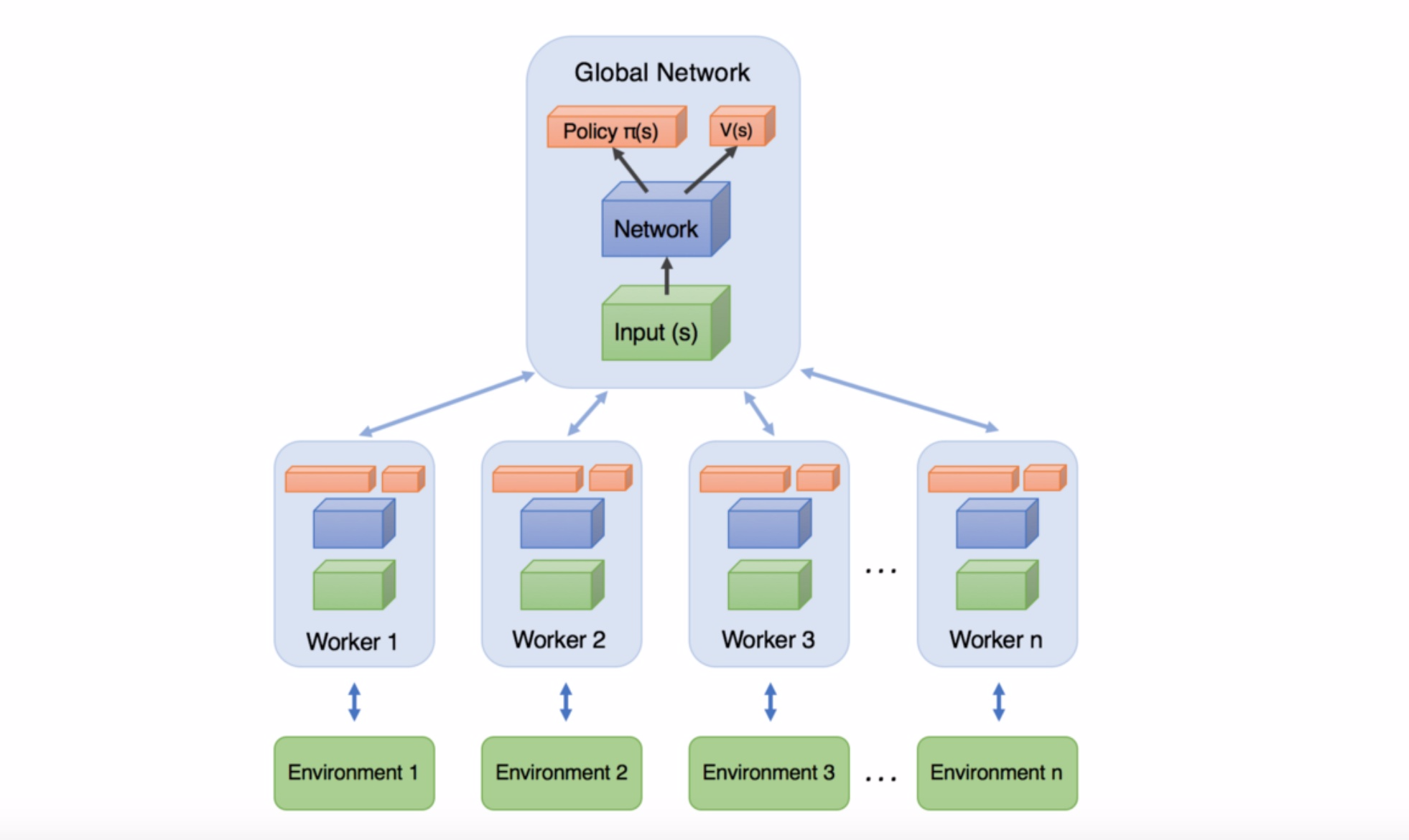其示意图可以用下图来描述 最后，A3C 的具体步骤如下 小结 本文跟随 Policy Based 算法的发展，简单介绍了过程中较为著名的 RL/DRL 算法。可以看出，不论是 PG -> DPG -> DDPG -> A3C，甚至包括上一篇文章介绍的 Q-learning ->DQN， 其实都有着很明确的逻辑链条（更多的是继承，以及每次一小步的突破），才终于缓慢进化到如今的 Alphago、Dota AI、StarCraft AI 等，每每想来总会感慨学术发展的不易。当然，限于水平与时间有限，RL/DRL 部分只能以极短的篇幅简单介绍，大家需要更深入的学习还是得回归论文与书籍。 尾巴 "当我们在谈论 Deep Learning"系列从开始写到现在大半年的时间，从最初的 Backpropagation，到超参数，再到架构如 CNN、RNN 等，再到 Unsupervised Learning，以及最后的 Reinforcement Learning 与 Deep Reinforcement Learning，算是基本完成了本人最初"对 Deep Learning 相关理论知识的简单梳理与介绍"的目标。同时在此，也对过程中提出改进建议与参与阅读的同学表示感谢！ 当然，新的系列仍然还是会写下去，只不过内容与形式我还没有确定下来，或许会换换口味哈哈。 本系列其他文章： 专栏总目录（新） via 当我们在谈论数据挖掘 - 知乎专栏 https://ift.tt/2FOtJF3 RSS6