编辑 | 陈大鑫
做理论需要的基础知识多,困难,周期长,没有直接经济效益,还只能一两个人单打独斗且无法使用大量计算资源,每个因素都和现在的主流发展方向(强调团队合作,强调速度和新闻性,代码开源,大数据,大量计算资源)背道而驰。 而且,理论研究论文大多艰深、晦涩难懂,结论依赖不现实的假设,难免令人望而却步乃至失望。相比之下,实验研究效果立竿见影,传播快。
田渊栋如此说道。
理论研究要让少数的、有情怀的人去做,远离市场噪杂和竞争,慢慢地钻研。“一万个硕士博士里有一个怀着这个理想,那迟早有一天会做出来的,大部分人不用费这个力气的。”
田渊栋又道。
昨日,NeurIPS 2020放榜,9454篇论文提交,1900篇接收,录取率仅为20.09%。
上海交通大学本硕、卡耐基梅隆大学机器人系博士,现任 Facebook 人工智能研究院(FAIR)研究员和研究经理的田渊栋这次投稿了三篇主打文章(一作或者最后一作),中了两篇。
田渊栋表示:还算不错。
得知自己中了两篇论文之后,作为知乎上的热爱分享、传播知识的大V,田渊栋第一时间写了两篇小博客各自介绍了这两篇篇论文:
第一篇设计了一个新的算法,来试图解决多智能体合作时联合优化策略的问题。
第二篇提出了一种新的黑盒优化的方法:LaMCTS (Latent Action Monte Carlo Tree Search),这个方法基于蒙特卡罗树搜索,但在这上面有改进。
AI科技评论第一时间联系到了田渊栋博士,经授权,现把内容整理如下。
在介绍两篇论文工作之前先把田渊栋博士的NeurIPS后感想转述如下:
这篇一作文章的理论在deadline前四天才被发现,在理论被发现之前,对策略变化的得分计算一直用的是一个极其复杂的方案,考虑各种状态进入和离开信息集的情况,光代码本身就写了一周,修理各种corner case修到头都秃了。最后实验上的效果也确实是单调上升,但一直证明不出来其正确性。 直到某一天晚上意识到根本不需要这么复杂,推出了非常简单的公式之后不敢相信自己的眼睛,立即重写代码,从晚上十点半写到十点四十分,跑出来的结果是一样的,速度还快。
数学的美,可能正是美在这里。 另一篇最后一作的中稿文章基本上我从头到尾都重写过一遍,包括abstract,introduction,方法还有实验部分。反观第三篇没中的,其实整体思路及实验效果都非常好,但因为写作只把关了abstract和intro,导致方法论的描述部分出现了低级失误,给reviewers造成了巨大的误解,可惜了。 做研究,文章其实贵精不贵多,现在铺天盖地的AI论文,每天看arXiv都看不完,但留下印象的,给领域提供实质性贡献的,其实并不多。
我每次向别人介绍FAIR内部的评价体系,都会说“我们不看论文数量”,每半年打绩效,只问有没有Top-3的工作,在每篇工作里的具体贡献是什么:思路是谁提出的?代码是谁写的?实验是谁跑的?效果是谁调上去的?定理是谁证的?文章是谁写的?其它的各种挂名文列上去就行,也没人会在意。这样算下来,花大力气发一篇好工作是正分,发一百篇毫无关联的水文是零分甚至是负的印象分,这样也可以鼓励大家多出成果少搭便车。
我也在向这方面一直继续努力。曾经挺羡慕那些文章列表上百的朋友们,但后来才明白什么才是自己想要走的道路。 之后的ICLR还会延续同样的模式,除开被拒转投的文章,还会有两篇新的文章出来,还是老样子,一篇一作,一篇最后一作。两篇文章都非常不错,而教师-学生的神经网络理论分析也将回归,用在一个大家想不到却正是极其适合的地方,得到极其有趣的结果,敬请期待。
接下来田渊栋博士对两篇中奖论文的介绍。
论文一
论文链接:https://ift.tt/3i94ArG
论文作者:Yuandong Tian, Qucheng Gong, Tina Jiang
这篇文章设计了一个新的算法,来试图解决多智能体合作时联合优化策略的问题。
对于不完美信息两人零和游戏,比如说两人德州扑克。
用现用的一些算法(比如说CFR)可以在理论上保证当迭代次数足够时一定收敛到纳什均衡点。但不完美信息多智能体合作的策略优化则要困难很多,并且往往会陷入局部极小值。
比如说有两个玩家合作,玩家1抽一张暗牌红桃A或黑桃A,然后向玩家2发一个红桃A或黑桃A或方块A的信号,让玩家2猜A手上的牌是什么,猜中得1分,猜不中则得0分。
显然在这种情况下,存在
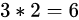 种协议,这6种协议是完全对称的,采用任何一种玩家2都可以猜中得1分。但如果规则稍微改一下,比如说发送黑桃A有0.1的附加分,那若玩家1和玩家2采用“抽红桃A发红桃A, 抽黑桃A发方块A”的协议,就赚不到这个附加分,是局部极小策略。但玩家1和玩家2单方面都不想改变自己的策略,因为单方面改变的结果是对方不理解自己策略的改变,导致得分的下降。
种协议,这6种协议是完全对称的,采用任何一种玩家2都可以猜中得1分。但如果规则稍微改一下,比如说发送黑桃A有0.1的附加分,那若玩家1和玩家2采用“抽红桃A发红桃A, 抽黑桃A发方块A”的协议,就赚不到这个附加分,是局部极小策略。但玩家1和玩家2单方面都不想改变自己的策略,因为单方面改变的结果是对方不理解自己策略的改变,导致得分的下降。
那在这种情况下,要如何去优化各自的策略呢?很多策略优化方案采用就是按坐标优化(Coordinate Descent),即假设其它人的策略不变,然后优化自身的策略。这显然在这里不太可行。而同时优化多个智能体的策略,在不完美信息的条件下,又是比较困难的,见下图:
这就使得策略与收益得分相互间的影响变得非常复杂,而且存在“牵一发而动全身”的关系,让联合优化变得非常困难——如果我们只想修改1000个信息集中的3个信息集的策略,那其它997个信息集上的期望得分也会发生变化,即便它们之上的策略并没有发生任何改变。
这篇文章的一个主要贡献,就是找到了一个”策略变化密度“(policy-change density)这样一个量,满足以下两个条件:
1、 不管上下游的策略是否发生了变化,如果一个状态的当前策略没有变化,那策略变化密度就为0。
2、策略变化密度在所有状态上的总和,就是整个游戏得分因策略变化后的改变量。
有了这两个性质之后,得分因策略变化后的改变量就可以分解成局部项了:如果只修改了3个信息集的策略,那么总的期望得分的增加就完全由这3个信息集上的策略变化密度的和来决定。这样就极大简化了计算。
策略变化后,整个游戏的得分改变量在每个信息集上的局部分解。
有了这个公式之后,再要联合优化策略就变得相对容易了。
这篇文章采用的是简单的深度优先搜索,从上游策略出发,先改变上游策略,然后给定上游策略,再改变下游策略,如此往复,然后看最后整个游戏的得分改变量的大小,最终选出最好的新策略组合。
这样就能达到联合策略搜索(Joint Policy Search)的目的,并且这样的算法得到的策略性能一定是单调上升的。
运用这个方法,我们先在一些小规模的非完美信息合作游戏(主要是桥牌叫牌阶段的简化版)上进行了测试。我们从CFR得到的联合策略开始,用搜索算法对当前的联合策略进行改进(CFR1k+JPS),直到陷入局部极大值为止。结果发现确实有用,新的策略都改进了得分,而且越复杂的游戏,改进越大。
这部分代码已经开源:
https://ift.tt/2Ym4g1T
最后当然是在真的桥牌叫牌环境下进行测试。
们先用A2C自对弈训练了一个还不错的基线策略,然后用上文提到的联合策略搜索(JPS)来改进队友间的叫牌约定,并且和目前较好的桥牌AI软件(WBridge5)进行了一千局开闭室比赛。
比赛是JPS和JPS一队,WBridge5和WBridge5一队。最后发现和基线策略相比,我们的效果确实变好了。
注意这里的两阶段训练没有用到任何人类对局,为的是能够无监督地学到全新的叫牌约定——让机器学到人类所不知道的新东西永远是很有意思的。
当然这里有个问题是我们只做了叫牌,没有做打牌,叫牌完了之后游戏就结束了,并以双明手(double-dummy)的分数,即所有牌摊开来打,来定胜负。
WBridge5是以正常叫牌加打牌的模式来优化的,并且事先也没有领教过我们学出来的新叫牌约定,所以这个比较不是特别公平(也被reviewer们使劲狂喷),但目前只有这个办法(这部分代码暂不开源,因为各种小trick比较多,之后等全部搞完了再说)。
论文二
论文链接:https://ift.tt/2HstjKW
论文作者:Linnan Wang, Rodrigo Fonseca, Yuandong Tian
(我们相关的工作还有一篇叫LaNAS,主要是将这个方法用在神经网络架构搜索(NAS)上:Sample-Efficient Neural Architecture Search by Learning Action Space https://arxiv.org/abs/1906.06832。Linnan Wang, Saining Xie, Teng Li, Rodrigo Fonseca, Yuandong Tian)
这篇主要是提出了一种新的黑盒优化(Black-box optimization)的方法。这个新的方法叫LaMCTS (Latent Action Monte Carlo Tree Search),顾名思义这个是基于蒙特卡罗树搜索(Monte Carlo Tree Search)的,但在这上面有改进。
传统的MCTS的目标是在给定状态空间(state space S)、行动空间(action space A)及状态转移函数(transition matrix, S, A -> S') 之后,通过搜索找到最优的行动序列,以获得最大的奖励。
MCTS搜索是通过增量构建一棵以初始状态
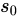 为根的树来实现的,树中的每个状态结点
为根的树来实现的,树中的每个状态结点
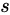 都有一个简单的模型
都有一个简单的模型
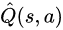 ,描述如果选择行动
,描述如果选择行动
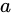 ,根据过去的经验会有多少奖励。新叶子结点的构建则权衡了过去的经验(exploitation)和探索新的结点(exploration)这两个目标,随着搜索的进行,新叶子会更多集中在有希望的区域里面。
,根据过去的经验会有多少奖励。新叶子结点的构建则权衡了过去的经验(exploitation)和探索新的结点(exploration)这两个目标,随着搜索的进行,新叶子会更多集中在有希望的区域里面。
乍一看,MCTS和规划有关,和黑盒优化似乎无关,那它们之间是如何建立联系的呢?
一般来说,黑盒优化都是从一个初始解出发,通过不停迭代来改进当前解,直到无法再改进为止。
其主要性能指标是:达到同样的函数值,需要多少次黑盒函数的调用,越少越好。因为在实际问题中,需要用黑盒优化的场景,往往是函数调用开销非常大且没有导数信息的场景,比如说函数值是一个复杂系统运转一天后的平均效率,或者是耗费巨资才可获得的一个实验结果,等等。
这个黑盒优化的迭代过程可以用各种方案去刻划:比如说从一个还不错的起始点开始的局部搜索,一个从粗到细的逐步精化,或者说局部渐进和长程跳跃的组合(例如进化算法的演化和突变),等等,每种方案都对应不同的行动空间。
但从本质上来说,优化和“下棋打游戏”等问题很大的不同点在于,优化本身没有”行动空间“的概念,对它而言,行动空间如何定义都无所谓,只要最终解质量好就行。
与其使用各种人工定义,自然的想法就是学一个行动空间出来。这就是这一系列文章的贡献。
我们以“解空间的切分”作为广义上的行动空间,而具体的切分方式,则是在每个MCTS的树结点上,用过去获得的样本点学一个最好的切分函数出来——我们希望这个切分函数能将好的和差的样本点尽量分开,这样一刀切下去,如果能将质量差的解空间统统切掉,以后少分配些搜索资源,那就是最理想的了。
而MCTS兼顾exploitation和exploration的特性,使得即便一开始切得不够好,以后也有扳回来重新划分空间的余地。而每个叶节点的空间,就是它的所有祖先节点的切分的交集。
以下是一个神经网络架构搜索(NAS)上的简单例子。
假设我们要搜索一个一至五层的卷积网络,每层的filter数是32或是64,filter大小可以是3x3或者5x5。考虑两个不同的行动空间,一个是逐层确定每层的参数(filter数及filter大小),另一个是先确定网络层数,再确定每层的参数。
从图上可以看到,明显是先确定网络层数的方案效率更高(同样样本下准确率更高),因为相对其它参数,层数对最后网络准确率的影响更大,如果先按层数切分搜索空间,那搜索效率自然就提高了。
洞察到了这些问题之后,我们提出了LaNAS和LaMCTS。
LaNAS采用线性函数切分空间,对于叶节点的函数值估计则采用简单的随机采样法,及最近比较流行的one-shot supernet。
LaMCTS做了改进,采用非线性函数切分空间,并且在叶节点上用了已有的黑盒优化的方法比如说Bayesian Optimization(BO)来找到叶节点的子区域里的最优解。
通过这个方式,特别对于高维问题达到同样性能,我们发现LaMCTS可以达到更低的样本复杂度。这里我们在Mujoco的任务上做了测试,和各种已有的黑盒算法进行了比较,蓝线是我们的方法:
LaMCTS在高维空间搜索中有优势,纵轴是奖励,越高越好。
当然LaMCTS和基于梯度的方法相比,在Mujoco的高维问题上还是有差距(因为Mujoco其实并不需要太多探索)。我们指出了自身的局限性,出乎意料地被reviewers们开口称赞。
因为每个叶结点采用了已有算法,LaMCTS也可以套在任何已知的黑盒优化算法上,作为一个元算法(meta-algorithm),让整个系统达到更好的效果。
为什么能提高呢?
主要原因是,传统方法像Bayesian Optimization (BO)在参数空间维数很大(比如上百维)的情况下,由于维数灾难的问题,高斯过程(GP)的建模效率就会大打折扣。
而LaMCTS通过切分空间,让GP的建模局限在一个比较小的范围内,从而提高了它的效率。
LaMCTS可以套在任何已知的黑盒优化算法上,一定程度上提高它们的性能。
田渊栋博士知乎链接:
https://ift.tt/3368oFQ
NeurIPS 2020录用结果已出,欢迎各位作者投稿
点击阅读原文,直达“CCF-NLP走进高校之郑州大学”直播页面!

没有评论:
发表评论