| 机器学习尤其是深度学习很难调试与修正,而最近谷歌大脑 Ian Goodfellow 等研究者发布了一个名为 TensorFuzz 的神经网络 Debug 开源库。他们将传统软件工程中由覆盖性引导的模糊方法引入到神经网络,并借助机器学习方法实现 Debug 过程。 神经网络正逐渐影响人类生活环境,包括医学诊断、自动驾驶、企业和司法决策过程、空中交通管制、以及电网控制。这些人类可以做到的事,神经网络也有可能做到。它可以拯救生命、为更多的人提供帮助。然而,在实现这些应用之前,我们首先需要确定神经网络到底是不是可靠的,因此它的修正和调试方法恰恰是我们现在所缺失的。 众所周知,由于各种原因,机器学习模型难以调试或解释,一是从概念上难以说明用户想要了解的模型信息,而且通过统计和计算也难以获得指定问题的答案。这个特性导致最近的机器学习出现「复现危机」,因为我们很难对不好调试的技术做出可靠的实验结论。 即使是与神经网络直接相关的简单问题也可能会有巨大的计算量,而且使用深度学习框架实现的神经网络也可能和理论模型相去甚远,所以神经网络非常难以调试。例如,ReluPlex 可以形式上地验证神经网络的一些特性,但由于计算成本太高,无法扩展到实际模型中。此外,ReluPlex 通过将 ReLU 网络描述为一个分段线性函数来进行分析,它使用一个矩阵乘法都为线性的理论模型。但实际上,由于浮点算法的存在,计算机上的矩阵乘法并非线性的,机器学习算法可以学习利用这种特性进行非线性运算。这并不是要批评 ReluPlex,而是想说明应该需要更多与软件直接交互地测试算法,以便更客观地测试因为深度学习框架而偏离理论的模型。 在 Ian Goodfellow 等人的这项研究中,他们使用传统软件工程已有的技术,即由覆盖性引导的模糊方法(coverage-guided fuzzing,CGF),并修正这种技术以用来测试神经网络。根据 Goodfellow 等研究者在原论文中所述,该项工作的主要贡献有以下几点: 为神经网络引入 CGF 概念,并描述了快速近似最近邻算法如何以通用的方式检查覆盖性。 为 CGF 技术构建了一个名为 TensorFuzz 的开源库。 使用 TensorFuzz 可在已训练神经网络搜索数值问题、在神经网络和对应经量化处理的网络间生成不一致性度量、在字符级语言模型中表现的不良行为。 下图描述了整体的 Fuzzer 过程,它与普通计算机程序的 CGF 结构非常相似,只不过它不与经检测的计算机程序交互,而是与 TensorFlow 的静态计算图进行交互。 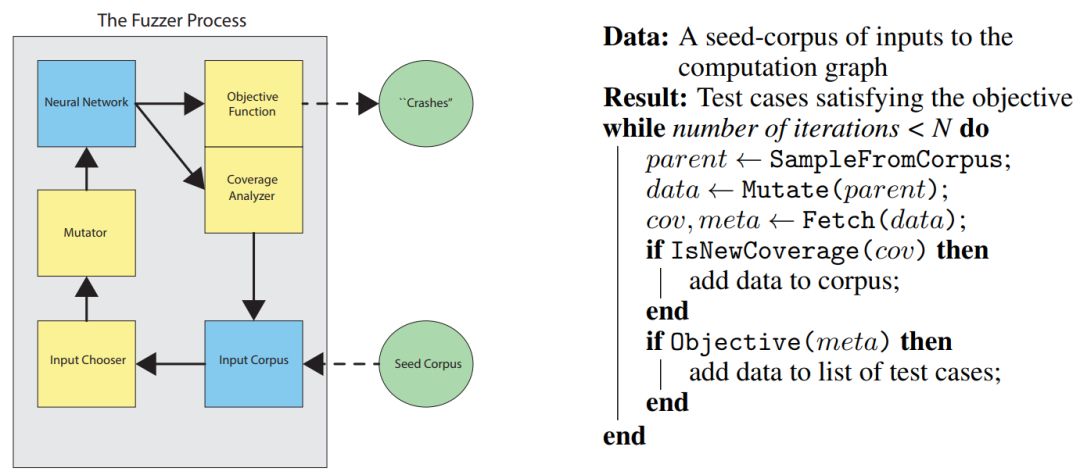
如上左图所示,Fuzzer 由 Seed 语料库开始,它为计算图提供至少一组输入。研究者将这些输入限制为有效的网络输入,例如对于图像输入,研究者可以限制输入数据有正确的图像尺寸和 RGB 通道数。在给定 Seed 语料库后,输入选择器将从输入语料库中选择不同的元素,例如输入选择器可以是以随机的方法选择输入。 给定有效的输入,Mutator 会对输入做一些修改,这种修改可能只是简单地翻转图像像素,同样也可以是在修改总量的某些约束下对图像进行修改。Mutator 输出的修改数据随后可以输入到神经网络中,TensorFuzz 需要从神经网络抽取出两种信息,即抽取一组元数据数组以计算目标函数,抽取一组覆盖性数组以计算实际覆盖性。计算覆盖性后,如果 Mutator 修改的数据需要执行覆盖,则将它添加到输入语料库中,如果计算的目标函数满足条件,则可以添加到测试案例列表中。 如上右图为 Fuzzer 主体过程的伪代码,在满足迭代数的情况下,从输入语料库中抽取样本为 parent,并使用 Mutate() 函数对该样本做修改以产生新的样本 data。样本 data 随后输入到神经网络,并通过 Fetch() 函数从该神经网络抽取覆盖性 cov 和元数据 meta 两个向量。接下来只需要通过 IsNewCoverage() 和 Objective() 两个函数判断 cov 和 meta 两个向量是不是满足条件,满足的话就能分别将 data 样本加入到输入语料库和测试案例列表。 以上只是 Fuzzer 主体过程的一般描述,Chooser、Mutator 以及 Fetcher 的具体结构与算法读者可详细查阅原论文。 论文:TensorFuzz: Debugging Neural Networks with Coverage-Guided Fuzzing 
论文地址:https://ift.tt/2AstWAs 众所周知,机器学习模型的解释和调试非常困难,神经网络更是如此。在本文中,我们为神经网络引入了自动化软件测试技术,该技术非常适合发掘仅在少量输入下出现的错误。具体而言,我们为神经网络开发了由覆盖引导的模糊(coverage-guided fuzzing,CGF)方法。在 CGF 中,神经网络输入的随机变化由覆盖性度量(coverage metric)引导,以满足用户指定的约束。我们描述了快速近似最近邻算法如何为神经网络提供这种覆盖性度量方法,并讨论了 CGF 在以下目标中的应用:在已训练神经网络中搜索数值误差、在神经网络和对应经量化处理的网络间生成不一致性度量、在字符级语言模型中表现不良行为。最后,我们发布了一个名为 TensorFuzz 的开源库,它实现了本论文所描述的技术。 4 实验结果 我们简要展示了 CGF 技术的一些应用以证实它的通用性质。 4.1 CGF 可以高效地找到已训练神经网络的数值错误 由于神经网络使用浮点数运算,它们对于训练期间及评估过程中的数值错误很敏感。众所周知,这些问题是很难调试的,部分原因是它们可能仅由一小部分很少遇到的输入所触发。这正是 CGF 能发挥作用的一个案例。我们专注于寻找导致非数(not-a-number,NaN)值的输入。并总结出如下结论: 找出数值错误很重要。数值错误,尤其是那些导致 NaN 的数值错误,假如在现实应用中首次遇到这些错误,重要系统将做出严重的危险行为。CGF 可以用于在部署系统之前找到大量的错误,并减少错误在危险环境中造成的风险。 CGF 可以快速找到数值错误。通过 CGF,我们可以简单地添加检查数值选项到元数据中,并运行我们的 fuzzer。为了测试这个假设,我们训练了一个全连接神经网络来分类 MNIST[26] 数字。我们故意使用了一个实现效果比较差的交叉熵损失函数,以增加数值错误出现的可能性。我们用 100 的 mini-batch 大小训练了 35000 个迭代步,直到达到 98% 的验证准确率。然后我们检查到,不存在导致数值错误的 MNIST 数据集元素。尽管如此,TensorFuzz 却在多个随机初始化中快速找到了 NaN,如图 2 所示。 基于梯度的搜索技术可能无法帮助寻找数值错误。CGF 的一个潜在缺陷是,基于梯度的搜索技术可能比随机搜索技术更加高效。然而,我们并不清楚如何明确基于梯度搜索的目标。目前不存在度量模型的真值输出和 NaN 值相似性的直接方法。 随机搜索在寻找某些数值错误方面是极度低效的。为了证实随机搜索不够高效且覆盖引导对于提高效率很有必要,我们对比了随机搜索方法。我们实现了一个基线随机搜索算法,并用 10 个不同的随机初始化在语料库的 10 万个样本上运行了该算法。基线算法在所有实验中未找到一个非限定元素。 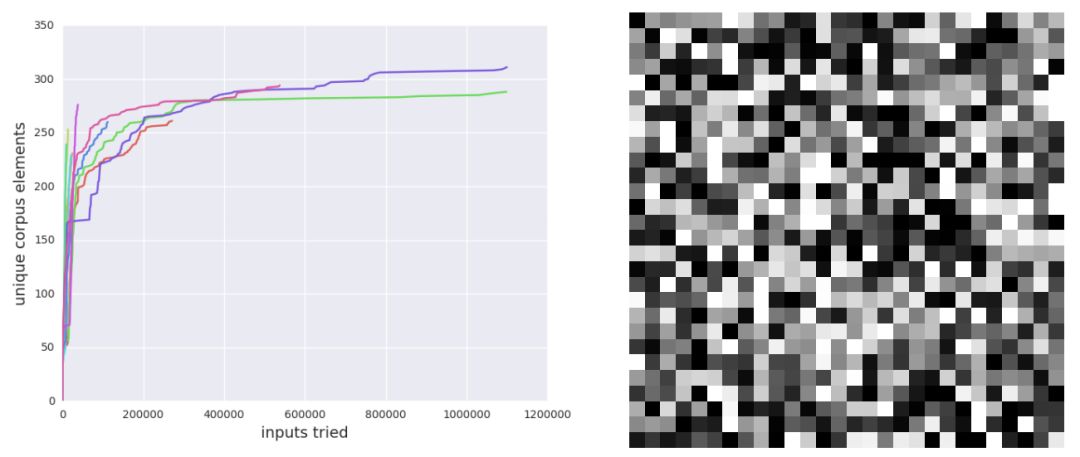
图 2:我们训练了一个包含某些不稳定数值运算的 MNIST 分类器。然后我们在 MNIST 数据集的随机种子上运行 fuzzer10 次。fuzzer 在每次运行中都找到了一个非限定元素。而随机搜索未能找到一个非限定元素。左图:运行过程中(共运行 10 次)fuzzer 的累积语料库大小。右图:由 fuzzer 找到的满足条件的图像示例。 4.2 CGF 解决模型和量化版本不一致的问题 量化(quantization)[18] 是一种神经网络权重被保存,且在执行神经网络计算的时候使用更少计算内存位数来表示数值的过程。量化常被用来减少神经网络的计算成本或大小。它还被广泛用于在手机的安卓神经网络 API 或 TFLite 上,以及在自定制机器学习硬件(例如谷歌的 Tensor Processing Unit[20])上运行神经网络推理。 寻找由量化导致的错误非常重要:当然,如果量化显著减少了模型准确率,那量化就没有什么意义了。给定一个量化模型,如果能检查出多少量化减少了准确率最好。 仅检查已有的数据只能找到很少的错误:作为基线实验,我们训练了一个使用 32 位浮点数的 MNIST 分类器(这一次没有故意引入数值错误)。然后把所有权重和激活值修剪为 16 位。之后,我们对比了 32 位和 16 位模型在 MNIST 测试集上的预测,没有找到任何不一致性。 CGF 可以快速在数据周围的小区域中找到很多错误:然后运行 fuzzer,变化限制在种子图像周围的半径为 0.4 的无限范数球中,其中仅使用了 32 位模型作为覆盖的激活值。我们将输入限制在种子图像附近,因为这些输入几乎都有明确的类别语义。模型的两个版本在域外的垃圾数据(没有真实类别)上出现不一致性并没有什么意义。通过这些设置,fuzzer 可以生成 70% 样本的不一致性。因此,CGF 允许我们寻找在测试时出现的真实错误,如图 3 所示。 随机搜索在给定和 CGF 相同的变化数量下无法找到新的错误:如 4.1 节所述,我们试验了一个基线随机搜索方法以表明覆盖引导在这种设置下特别有用。随机搜索基线在给定和 fuzzer 相同的变化数量下无法找到新的任何不一致性。 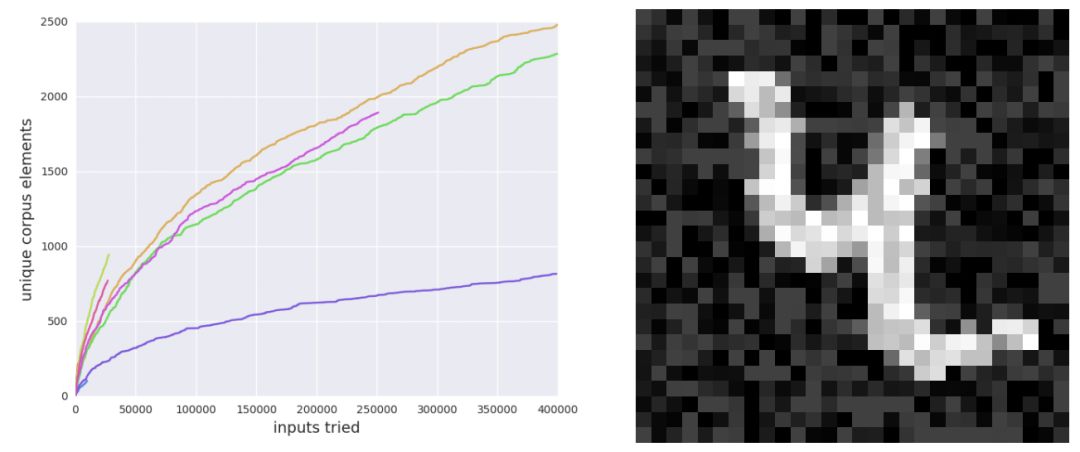
图 3:我们训练了一个 32 位浮点数的 MNIST 分类器,然后将对应的 TensorFlow 图修剪为 16 位浮点数图,原始的和修剪后的图都在 MNIST 测试集的全部 10000 个元素上执行相同的预测,但 fuzzer 可以找到大约 70% 的测试图像中半径为 0.4 的无穷范数球中的不一致性。左图:fuzzer 的累积语料库大小随运行次数(共 10 次)的变化。那些一路朝右的曲线对应失败的模糊化(fuzzing)运行。右图:由 fuzzer 找到的被 32 位和 16 位神经网络分类为不同类别的图像。 ]]> 原文: https://ift.tt/2M50PV7 | 
没有评论:
发表评论