AI 人工智能新闻资讯: 当我们在谈论 AI 作画：风格迁移

2018年8月5日星期日

当我们在谈论 AI 作画：风格迁移

引言

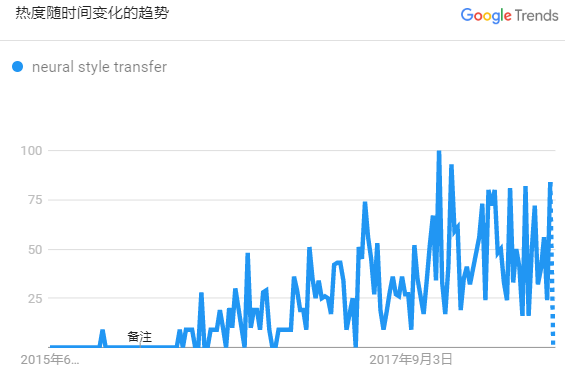
"风格迁移"相信大家都不陌生，最常见的形式就是将一张普通的图片转换为各种艺术风格图片。"风格迁移"本身并不是新课题，但是借助 Deep Learning 其效果大幅提升，变得实用起来。从 Google Trends 可以看到，其热度从2015年末开始一路攀升，甚至出现了火爆的"风格迁移"滤镜 app——Prisma。下面，我们将通过几篇文章，简单回顾一下"风格迁移"的发展，并实践看看它们是否足够智能。

Per-Image-Per-Model

让我们回到2015年，由 CNN 带动起的这一波 AI 浪潮还在如火如荼的进行着：各种基于 CNN 的更强大的架构还在不停地被提出、ILSVRC 的屠榜活动也完全没有减弱的迹象、所有人都觉得这次智能时代真的要到来了。这一块的详细介绍可以参考"当我们在谈论 Deep Learning：CNN 其常见架构（上）"、"当我们在谈论 Deep Learning：CNN 其常见架构（下）"两篇文章，在这里先略过。在这种全民屠榜的时代，也会出现一些"不务正业"的学者，比如 Leon A. Gatys。 Gatys 在"A neural algorithm of artistic style.2015"提出了一种新技术：利用 CNN 来将一张普通图片转换成艺术画，如下图。他可能不曾想到的是，这项技术会发展出一个百亿市值的app——Prisma，这是后话了。我们先来介绍下这篇有趣的文章。

基本思路

事实上，文章的做法非常朴素：

Loss 定义：由于希望输出图片保留着 Content Image 的内容以及 Style Image 的风格，作者定义了两种 Los：Content Reconstruction Loss、Style Reconstruction Loss。它们分别对应着输出图片与 Content Image 内容上的差异，以及与 Style Image 在风格上的差异。最终的 Loss 为两种 Loss 的加权和，权重用于调节希望更倾向于内容相似，抑或是风格相似
输入及输出：输入为高斯噪声图像，通过不断改变输入图像的像素值来优化 Loss，最终得到的图像即输出结果
优化方法：万能的 Gradient Descent，即通过 BP 来优化输出图像的像素值，当 Loss 稳定时停止迭代

接下来，我们详细介绍下网络结构，与 Loss 的具体定义。

网络结构

作者使用的是训练好（Pre-Train）的 VGG-19 网络。VGG 网络源自"Very Deep Convolutional Networks for Large-Scale Image Recognition. 2014."，原文中被用于图片识别。由于训练好的 CNN 可以看成是对图像特征提取器（类比基于规则的特征提取），因此 Pre-Train VGG 也经常被用于提取图片特征。这里作者使用的是 VGG-19，其网络由大量 3*3 Convolution Layer(stride=1) 和 2*2 Max-Pooling Layer(stride=2)组合而成，其结构示意图如图：

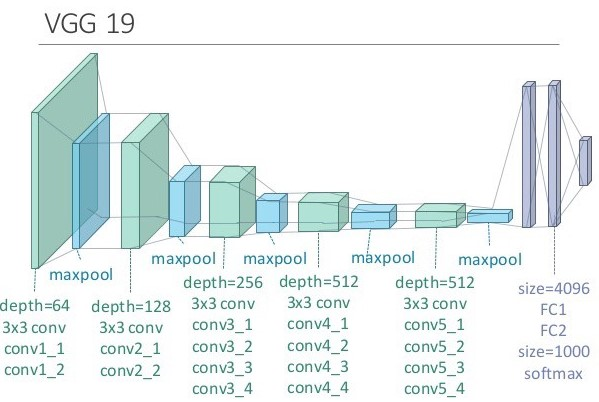
当然，作者在调参的过程中对 VGG-19 结构也做了些细微改变，这些调参细节这里不再赘述。

Loss 定义

Content Loss

如上面所说，由于希望输出图片保留着 Content Image 的内容以及 Style Image 的风格，作者定义了两种 Loss：Content Reconstruction Loss 和 Style Reconstruction Loss。我们先明确一下定义， x 表示输入图像， p 表示输出图像， l 表示 VGG 中的第 l 层。对于 VGG 第 l 层，假设有 N_l 个 filter，每个 filter 输出的 feature map 大小为 M_l （feature map 的长宽积）。这时，第 l 层的 layer 输出的 N_l 个大小为 M_l feature map，用一个 N_l*M_l 的矩阵 F^l 来记录。 F^l_{ij} 表示第 l 层，第 i 个 feature map 的第 j 个 activation 的值。

于是 Content Reconstruction Loss 可以表示为

L_{content}(p,x,l)=1/2 \sum_{i,j} (F_{ij}^l - P_{ij}^l)^2

Style Loss

比较有趣的是 Style Reconstruction Loss，作者创造性的以第 l 层 N_l 个 feature map 之间的 Gram Matrix 作为它们风格描述。Gram Matrix 的定义如下

在本文中，上图的 A^T 就是第 l 层 layer 中的矩阵 F^l。若令 a,x 分别表示输入图像、输出图像， A^l,G^l 分别为它们第 l 层的风格描述，则第 l 层的 Loss E_l 定义为

E _ { l } = \frac { 1 } { 4 N _ { l } ^ { 2 } M _ { l } ^ { 2 } } \sum _ { i , j } \left( G _ { i j } ^ { l } - A _ { i j } ^ { l } \right) ^ { 2 }

多 Layer 的总 Style Reconstruction Loss 则可以表示为

\mathcal { L } _ { s t y l e } ( a , x ) = \sum _ { l = 0 } ^ { L } w _ { l } E _ { l }

相信不少同学跟我一样，对 Gram Matrix 为什么能够作为风格描述比较疑惑。事实作者在文中也没有解释，但在Quora中有同学提到过 Gatys 在其他场合有过解释，虽然我并没有找到原始出处（因此无法保证真实性），还是放在这里供大家参考

"Gatys when asked why gram matrix at a talk said that the Gram matrix encodes second order statistics of the set of filters. it sort of mushes up all the features at a given layer, tossing spatial information in favor of a measure of how the different features are correlated." - Siraj Raval

如果觉得上述定性理解并不令人信服的同学，还可以查看"Demystifying Neural Style Transfer"这篇文章，作者从优化的角度对 Gram Matrix 的有效性进行了解读。

Total Loss

有了上述 Content Loss、Style Loss，Total Loss 的定义也就呼之欲出了。令 p,a,x 分别表示 Content Image、 Style Image、以及输出图像，则 Total Loss 定义为

\mathcal { L } _ { t o t a l } ( p,a,x ) = \alpha \mathcal { L } _ { c o n t e n t } (p , x) + \beta \mathcal { L } _ { s t y l e } ( a, x )

效果测试

这里我们以两组图像为例，看看这篇文章的效果如何。

对于 AI 类实验，首先当然邀请我的 AI 女神 Makise Kurisu（牧濑红莉栖），就拿她那张发表演讲的照片作为 Content Image 吧！Style Image 就选择毕加索的这幅"Reclining Woman 1954"，结果如下

可以看出，得益于 Style Image 的风格较为简单，人物主体部分风格确实已经跟"Reclining Woman 1954"比较相似了，这里主要体现在颜色（近似）以及线条（较粗放）上。不过缺点也是有的，比如背景上多了一些莫名其妙的线条，以及 Kurisu 那怨念的眼神。。。

为了避免被女神揍，接下来我们再看一组静物的效果。

这一次， Style Image 几乎是由纯色块构成的，很少出现渐变色；而 Content Image 背景有一定复杂度（较多不规则污渍），且构图难以通过色块表达，为了向 Style Image 靠近，输出图像产生了一系列畸变。虽然效果并不算很好，但是我意外地喜欢这种畸变的效果！

所以，风格这种东西，存在一定的主观性，较难评价。作为 Neural Style Transfer 的开山鼻祖，它最大的意义在于率先开辟了这条有趣的道路。而它最大的缺点，就是实在是太慢了，对于每一组 Content Image 和 Style Image，永远都需要重新训练（好几个小时），这个代价是不可接受的。所以，大量后来者开始向这方面努力。

Per-Style-Per-Model

时间来到2016年，GoogLeNet、ResNet 等更强大的架构已经争先恐后地被提出来。虽然曾经的王者 VGG 才诞生才两年不到，这时候回头看它朴素地俨然上个世纪的产物。这时，"风格迁移"也已经不是新鲜事了，但如上文所述，Gatys 文章提出的方法速度实在太耗时了。借助如今更强大的网络架构，是否有可能在保持质量的情况下，提高"风格迁移"的速度呢？李飞飞团队成员 Johnson 的文章"Perceptual losses for real-time style transfer and super-resolution. 2016"正是希望缓解这个问题。

在此文章中，Johnson 提出了一个新的网络结构，同时用于解决"风格迁移"与"图像超分辨率"的问题，下面我们仅介绍与"风格迁移"相关的部分。

基本思路

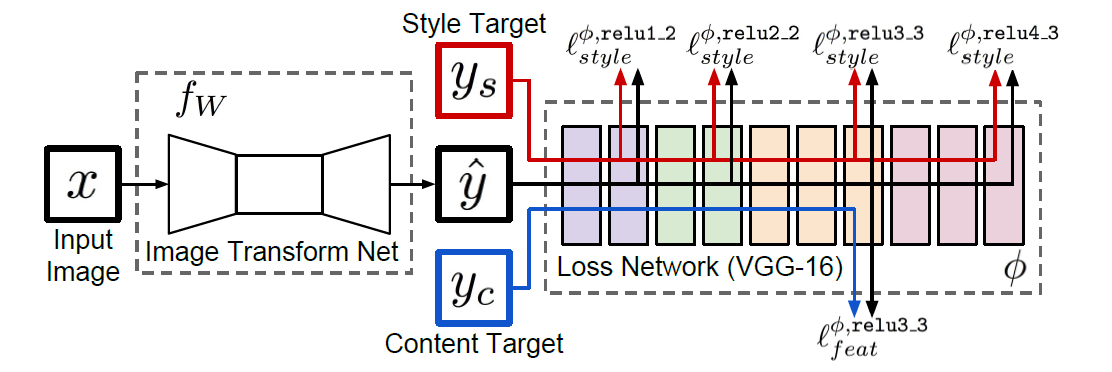
Johnson 提出的网络结构如上图，不同于 Gatys 文章中仅有一个网络（VGG-19），这里本质包含两个网络：图像的生成网络（Image Transform Net）与 Loss 计算网络（Loss Network）。基本思路如下：

1. 在训练阶段，输入为大量 Content Image 与一张 Style Image（因此一个模型只能训练出一种风格）。每次输入一张 Content Image 图像和一张 Style Image，这里将它们表示为 \left\{ y _ { i } \right\} 。对 Content Image x ，利用 Image Transform Net 进行"风格迁移"生成 f_W(x) ，并通过 Loss Network 计算 Loss（可能包含多个不同定义的 Loss， { \ell _ { 1 },..., \ell _ { k }} ）。接下来通过 GD 优化下面的目标

W ^ { * } = \arg \min _ { W } \mathbf { E } _ { x , \left\{ y _ { i } \right\} } \left[ \sum _ { i = 1 } \lambda _ { i } \ell _ { i } \left( f _ { W } ( x ) , y _ { i } \right) \right]

2. 在测试阶段，将 Content Image 图像输入 Image Transform Net，输出 f_W(x) 则为"风格迁移"后的图像

3. 文章中 Loss 的定义与 Gatys 近似，也主要包含 Feature Reconstruction Loss.、Style Reconstruction Loss 两个方面，这在后面详细介绍

网络结构

Image Transform Net

Image Transform Net 的结构主要由 Convolution Layer 和 Residual Block 组成，具体如下表。

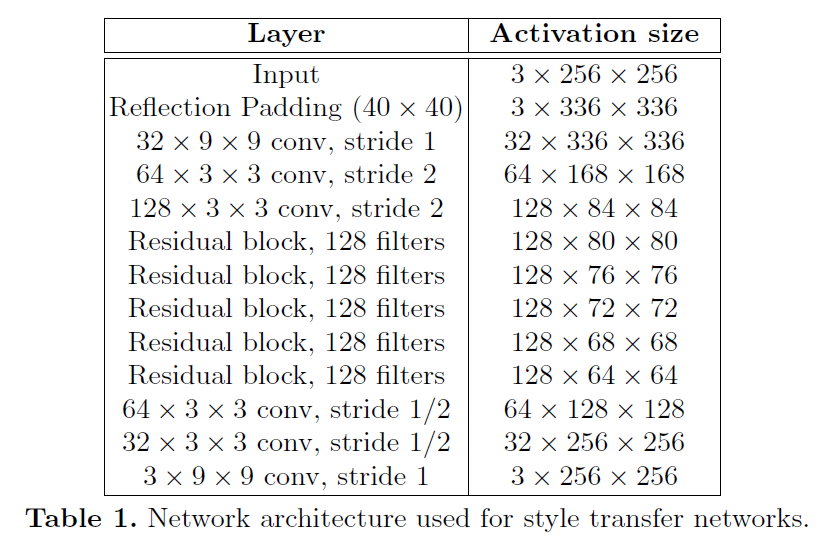
其中有几点需要说明：

作者为了减少计算量，同时也为了扩大 Convolution Kernel 能够影响的区域大小，通过对输入图像先进行下采样，再进行上采样的方式来获得原图大小的输出图像。关于下采样部分比较好理解，即上图中的两个 stride=2 的 Convolution Layer。对于上采样，作者使用了两个 stride= \frac{1}{2} 的 Convolution Layer，或者可以称作是 stride=2 的 Transposed Convolution Layer。Transposed Convolution 的概念非图像领域的同学可能比较陌生，可以参考"Transposed Convolution, Fractionally Strided Convolution or Deconvolution"，我就不再对其定义赘述了。
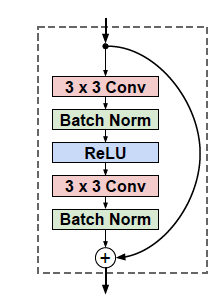
其时 RestNet 已经被提出（RestNet 的具体介绍可以参考"当我们在谈论 Deep Learning：CNN 其常见架构（下）"），Residual Block 已被证明在较深网络中更容易优化。同时对于"风格迁移"这类任务，输入图像与输出图像相似度比较高，"Residual Block 更易表达恒等变换"的性质也较为适用此种场景。本文所使用的 Residual Block 结构如下图
其他细节如采用了 Batch Normalization 来降低优化困难（Batch Normalization 的介绍与有点可以参考"当我们在谈论 Deep Learning：DNN 与它的参数们（叁）"）等这里也不再详细描述。

Loss Network

Loss Network 其实就是 Pre-Trained VGG-16。按照文中的说法，VGG的 weight 在本实验中训练阶段也是固定的（测试阶段根本不会用上）。所以，这里可以认为 VGG 是一种固定的特征提取方式，方便计算 Feature Reconstruction Loss.、Style Reconstruction Loss。VGG-16 的具体结构这里就不再赘述了，详细可以参考"Very Deep Convolutional Networks for Large-Scale Image Recognition. Computer Science, 2014."。

Loss 定义

Feature Reconstruction Loss

令 \hat { y } 为 Image Transform Net 的输出图像， \phi 为 Loss Net（VGG-16），Content Image 为 y 。有 \phi _ { j } ( y ) 为 Content Image 在 Loss Net 中第 j 层的 activation，形状为 C _ { j } H _ { j } W _ { j } ，即 Channel、Height、Width。与 Gatys 文章的定义类似，Feature Reconstruction Loss 定义为某个 Convolutional Layer 中 y,\hat { y } 的差异，即

\ell _ { f e a t } ^ { \phi , j } ( \hat { y } , y ) = \frac { 1 } { C _ { j } H _ { j } W _ { j } } \left\| \phi _ { j } ( \hat { y } ) - \phi _ { j } ( y ) \right\| _ { 2 } ^ { 2 }

Style Reconstruction Loss

同样与 Gatys 文章的定义类似，每一层 Convolutional Layer 的风格使用不同 Channel 的 Feature Map 的 Gram Matrix 来描述，Style Reconstruction Loss 则定义为 Gram Matrix 的 F 范数，具体公式如下

\begin{align} & G _ { j } ^ { \phi } ( x ) _ { c , c ^ { \prime } } = \frac { 1 } { C _ { j } H _ { j } W _ { j } } \sum _ { h = 1 } ^ { H _ { j } } \sum _ { w = 1 } ^ { W _ { j } } \phi _ { j } ( x ) _ { h , w , c } \phi _ { j } ( x ) _ { h , w , c ^ { \prime }} \\ & \ell _ { s t y l e } ^ { \phi , j } ( \hat { y } , y ) = \left\| G _ { j } ^ { \phi } ( \hat { y } ) - G _ { j } ^ { \phi } ( y ) \right\| _ { F } ^ { 2 } \\ \end{align}

Total Variation Regularization

为了令输出图像平滑，作者还参考 "Understanding deep image representations by inverting them.2015."中的定义，为 Total Loss 增加了正则项。对于一个图像 x ， x _ { i j } 表示 i,j 坐标处的像素值，Total Variation Regularization 定义如下

{\ell}_ { TV } ( \mathbf { x } ) = \sum _ { i , j } \left( \left( x _ { i , j + 1 } - x _ { i j } \right) ^ { 2 } + \left( x _ { i + 1 , j } - x _ { i j } \right) ^ { 2 } \right) ^ { \frac {1 } { 2 } }

Total Loss

最终，Total Loss 的定义呼之欲出，即

\ell _ { total } = \lambda _ { c } \ell _ { f e a t } ^ { \phi , j } \left( y , y _ { c } \right) + \lambda _ { s } \ell _ { s t y l e } ^ { \phi , J } \left( y , y _ { s } \right) + \lambda _ { T V } \ell _ { T V } ( y )

其中 y, y_c, y_s 分别表示 Image Transform Net 的输出图像，Content Image，Style Image。 \ell _ { s t y l e } ^ { \phi , J } ( \hat { y } , y ) 表示多个 Layser 的 Style Reconstruction Loss 之和， J 表示 Layer 的集合。

效果测试

可以看出，此文章中训练好一种风格的 Model 后，当需要进行"风格迁移"时，仅需要进行 Forward Propagation 即可，速度优势非常明显。而且按照文章中的例子，其生成图像的质量与 Gatys 不相上下。这里我以几组照片看看它的具体效果。

仅从上面这一组图上看，Johnson 提出的方案在细节保留的能力非常恐怖（尤其是结果1和3），其效果也几乎都是我期望的输出。不知道是否是得益于更多的训练数据，部分结果质量甚至超出我的预期，当然不排除是小数据下的巧合。但是不得不说，这样的结果已经让我有利用模型来生成壁纸的欲望了。

其他

上面介绍了 Per-Image-Per-Model、Per-Style-Per-Model，Model 在保持质量的同时提高效率与通用性。下一步是如何更进一步，能将多种、甚至任意 Style 都通过一个 Model 来表达。我本已选择了较近期的一篇文章，"Universal style transfer via feature transforms.2017"，作为例子讲解。然而，阅读后才发现文章最核心的"feature transforms"部分并非通过 Deep Learning 实现，而仅是通过简单地矩阵分解与变换实现，这种方式对于复杂图像很可能会丢失信息，限制通用性。通过简单几个实验，我也感觉到这种情况确实存在，具体结果如下。由于结果并不太符合预期，在此就不再详细介绍，相信后面很快会有改良的方案提出。

效果测试